1+2+3+.... to ∞ = -1/12 and Sum of a Series
- Shrijak Dahal

- Jun 9, 2020
- 2 min read
Updated: Jun 14, 2020
Have you ever realized what will happen if we sum all the natural numbers up to infinity?
1 + 2 + 3 + 4 + .... to ∞ = -1/12
The sum of all natural numbers added up to infinity is expected to be a very large number but came to be a negative fraction. Yes, Mathematics is fun and to your query, this blog is the solution. Now, let's see the supposed proof that 1+2+3+.... to ∞ = -1/12 (Taken from Numberphile) :

This series is called Ramanujan Summation.
The Ramanujan Summation also has had a big impact in the area of general physics, specifically in the solution to the phenomenon known as the Casimir Effect. Hendrik Casimir predicted that given two uncharged conductive plates placed in a vacuum, there exists an attractive force between these plates due to the presence of virtual particles bread by quantum fluctuations. In Casimir’s solution, he uses the very sum to model the amount of energy between the plates. And there is the reason why this value is so important.
Now, to the next part:
We know the formula for the sum of n natural integers is n(n+1)/2. i.e.,
1+2+3+........+n = n*(n+1) / 2

So,
By given equation (c),

So, if n tends to infinity then, ∞ should be -0.2113 or -0.7886.
Which is absurd. So, simply the summation of natural numbers till infinity is undefined.
We can see it by looking at equation (a) too. As the series is oscillatory it's values oscillates between 0 and 1 and saying its summation till infinity is 1/2 isn't valid. And, both series (b) and (c) are divergent so, their sum is simply undefined.
So, why is this summation very important?
The wrong result appeared in the work of the famous Indian mathematician Srinivasa Ramanujan in 1913. But Ramanujan knew what he was doing and had a reason for writing it down. He had been working on what is called the Euler zeta function.
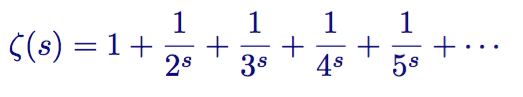
The corresponding sum converges to a finite value as long as s is a number greater than 1. For every s>1, the expression zeta(s) has a well-defined, finite value. zeta(s) is what’s called a function, and it’s called the Euler zeta function after the prolific 18th-century mathematician Leonhard Euler.
For example if s = 2,
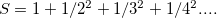
If we take the partial sum of this series,
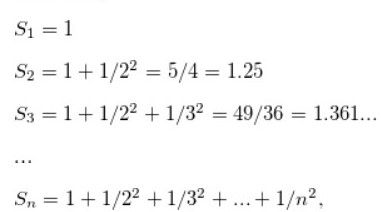
So, if we sum all the numbers it gets arbitrarily close, without ever exceeding, the number 1.644934 (pi squared over 6). So, the sum converges to 1.644934 for s=2.
But, what if we plug in the value for s that is less than 1: the sum diverges.
But there is also another thing we can do. Using some high-powered mathematics known as complex analysis there is a way of extending the definition of the Euler zeta function to numbers s less than or equal to 1 in a way that gives you finite values. This method of extension is called analytic continuation and the new function we get is called the Riemann zeta function, after the 19th-century mathematician Bernhard Riemann.
See the amazing visualization of the Riemann hypothesis and analytic continuation by 3blue1brown Here.
So, if we put the value for s = -1 in the Riemann zeta function we get a finite output.
And you guessed it,
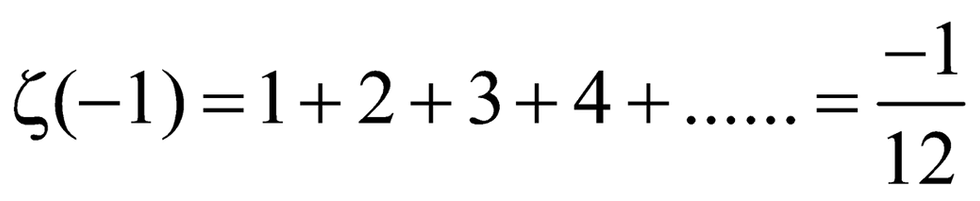
This is one way of making sense of Ramanujan’s mysterious expression.



Comments